Комплекс математических моделей эффективного администрирования системы беспроводного доступа в сеть интернет
Рассматриваются существующие варианты передачи данных в глобальных и беспроводных сетях. В работе предложена концепция использования промежуточного блока администрирования передачи данных при организации публичного беспроводного доступа в Интернет по технологии Wi-Fi, которая предполагает в процессе реализации получить данные через промежуточную сеть. Представлен комплекс математических моделей, описывающий возможные режимы администрирования. В целом, эти модели позволяют устанавливать значимые параметры и рассчитать их критические значения, что в свою очередь позволяет установить «решающие правила» для организации оптимального администрирования в информационной системе.
Ключевые слова: беспроводные сети, Интернет, информация, бизнес, образование, компьютеры, передача данных, общество, теория массового обслуживание, численный эксперимент, режимы администрирования
На сегодняшний день наблюдается активный рост пользованием Интернетом посредством беспроводных технологий. Это обусловлено ростом мобильных устройств и современными требованиями, т.е. рабочая и учебная деятельность стремительно преобразуется в электронный формат.
Интернет по технологии Wi-Fi получил широкое распространение, начиная от сферы услуг до глобальных бизнес-проектов и в тоже время, в основном, он является платным. Тем не менее, многие организации, работающие в сфере услуг, предоставляют бесплатный доступ в Интернет по технологии Wi-Fi с целью привлечения клиентов, и тем самым надеясь увеличить рентабельность своего бизнеса, однако весьма часто такая услуга оборачивается убытком для этой компании. Очевидно, рентабельность этой услуги можно достичь за счет увеличения массовости доступа в Интернет путем эффективного администрирования.
Рассмотрим предложенную систему как совокупность взаимосвязанных компонентов [3]: пользователь (П) беспроводной сети, беспроводной Wi-Fi коммутатор (К) и сервер (С) с предустановленным компонентом обработки данных. Порядок ее функционирования полностью описывается приведенной ниже последовательностью этапов.
1. Клиент приходит в место публичного доступа к Интернет с любой технической аппаратурой, поддерживающей технологию Wi-Fi.
3. При поиске беспроводных системы он обнаруживает точку доступа с незащищенным подключением.
4. Подключившись к этой точке, пользователь изначально ограничен в доступе к Интернет. При введении любого адреса в программе-браузере, его автоматически перенаправляют на web-страницу, размещенную на посреднической странице, где генерируется содержимое страницы в зависимости от географического расположения устройства.
5. Страница содержит информацию, которую необходимо донести до конечного пользователя; право составления и изменения предоставляемой информации имеет только владелец беспроводного устройства.
6. На странице размещена кнопка, которая осуществляет разрешение доступа клиента в Интернет.
7. Пользователь беспроводного подключения может получить доступ в Интернет, только при нажатии кнопки активации
8. Доступ в Интернет может быть разрешен в течение определенного времени, а так же с ограничением скорости доступа. Во время посещения всех страниц, у пользователя автоматически генерируется в нижней части экрана информационный блок с 15 % заполнением от высоты рабочего окна программы веб-браузера. В отображаемом блоке владелец беспроводного устройства может изменять и добавлять информацию через удалённый сервис путем авторизации учетных данных с привязкой конкретного устройства.
Для реализации этой концепции построим комплекс математических моделей описывающие различные режимы администрирования
Рассмотрим возможные ситуации и опишем предложенную систему в терминах теории массового обслуживания [1,2,4].
1. Администратор никак не ограничивает количество заявок, и любой клиент имеет возможность беспрепятственного доступа в систему и подключения к сети Интернет. Это система массового обслуживания с бесконечным числом каналов. Граф ее представлен на рис. 1.
 ,
,
Рисунок 1. Граф системы с бесконечным числом каналов
где μ вычисляется по формуле
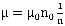 ,
,
если число действующих каналов больше 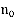 и
и 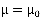 - если число каналов не превосходит
- если число каналов не превосходит 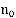 .
.
Финальные вероятности такой системы 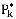 вычисляются по формулам Эрланга
вычисляются по формулам Эрланга 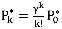 , где
, где 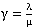 , а
, а 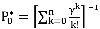 .
.
В результате численного эксперимента было установлено, что при увеличении интенсивности входного потока система в скором времени прекратит функционировать, т.е. вследствие снижения интенсивности обслуживания среднее время пребывания заявки в системе станет неприемлемо большим и процесс обслуживания фактически прекратится, если администратором не будут приняты соответствующие меры.
2. Администратор допускает к соединению с Интернет не более 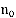 пользователей одновременно, когда все сформированные каналы обслуживания функционируют с неснижаемой интенсивностью
пользователей одновременно, когда все сформированные каналы обслуживания функционируют с неснижаемой интенсивностью 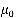 . Клиенты, пожелавшие воспользоваться услугой системы аппаратно-программного комплекса промежуточной сети передачи данных при организации публичного доступа в сеть Интернет в которой уже находится
. Клиенты, пожелавшие воспользоваться услугой системы аппаратно-программного комплекса промежуточной сети передачи данных при организации публичного доступа в сеть Интернет в которой уже находится 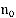 заявок, помещаются в очередь, и подключаются к обслуживанию по мере освобождения каналов. Число мест в очереди не лимитируется. Это типичная многоканальная система массового обслуживания с бесконечным ожиданием, граф которой представлен на рис. 2.
заявок, помещаются в очередь, и подключаются к обслуживанию по мере освобождения каналов. Число мест в очереди не лимитируется. Это типичная многоканальная система массового обслуживания с бесконечным ожиданием, граф которой представлен на рис. 2.

Рисунок 2. Граф системы с бесконечным ожиданием
Все расчетные соотношения для определения функциональных характеристик систем подобного типа известны и здесь приводятся только те из них, которые были использованы в ходе численного эксперимента, не касаясь технических потребностей их получения. Финальная вероятность состояния 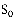 , когда система свободна, вычисляется по формуле
, когда система свободна, вычисляется по формуле 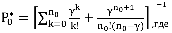
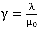 ,
,
а вероятность всех прочих состояний
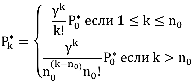
Средняя длина очереди (клиентов ожидающих подключения к Интернет) для этой системы
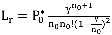 ,
,
а среднее время пребывания в очереди
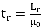 .
.
В ходе численного эксперимента для этой модели показано, что при росте интенсивности входного потока и при уменьшении интенсивности обслуживания 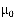 , величина
, величина 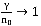 и длина очереди
и длина очереди 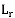 при этом неограниченно возрастает. Это приводит к прекращению функционирования системы вследствие ее переполнения. Следовательно, администратор системы должен контролировать работоспособность системы и в случае достижении критической длины очереди необходимо в принудительном порядке перезапустить систему.
при этом неограниченно возрастает. Это приводит к прекращению функционирования системы вследствие ее переполнения. Следовательно, администратор системы должен контролировать работоспособность системы и в случае достижении критической длины очереди необходимо в принудительном порядке перезапустить систему.
3. Количество формируемых каналов обслуживания не превышает 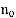 , что обеспечивает комфортные условия работы, однако, клиенты, попавшие в очередь, ведут себя не столь пассивно, как в варианте 2. Потеряв какое то время в очереди, часть клиентов уходит из системы, не дождавшись предоставления канала подключения к Интернет. Это, так называемая, модель с «нетерпеливыми» заявками.
, что обеспечивает комфортные условия работы, однако, клиенты, попавшие в очередь, ведут себя не столь пассивно, как в варианте 2. Потеряв какое то время в очереди, часть клиентов уходит из системы, не дождавшись предоставления канала подключения к Интернет. Это, так называемая, модель с «нетерпеливыми» заявками.
Для анализа работы систем с «нетерпеливыми» заявками, как правило, принимается гипотеза о том, что время ожидания клиента в очереди есть случайная величина, подчиняющаяся экспоненциальному закону распределения с параметром 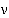 . Иначе говоря, среднее время пребывания заявки в очереди
. Иначе говоря, среднее время пребывания заявки в очереди
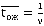 .
.
Таким образом, 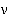 - имеет смысл интенсивности потока заявок, покидающих систему, но не получивших обслуживания. На рис.3 представлен граф такой системы
- имеет смысл интенсивности потока заявок, покидающих систему, но не получивших обслуживания. На рис.3 представлен граф такой системы

Рисунок 3. Граф системы с «нетерпеливыми» заявками
Финальная вероятность пребывания системы в состоянии 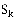 при
при 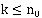 определится по формуле
определится по формуле 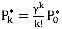 , где
, где 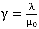 .
.
Если же все каналы сформированы и имеет место накопление очереди, то
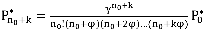 , где
, где 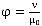 , а
, а
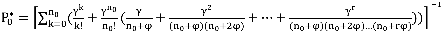 (5)
(5)
Ряд в квадратных скобках сходится при любом 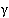 , что исключает возможность неограниченного возрастания числа заявок в очереди и нарушения функционирования системы аппаратно-программного комплекса промежуточной сети передачи данных при организации публичного доступа в сеть Интернет по этой причине.
, что исключает возможность неограниченного возрастания числа заявок в очереди и нарушения функционирования системы аппаратно-программного комплекса промежуточной сети передачи данных при организации публичного доступа в сеть Интернет по этой причине.
Однако, в отличие от модели 2, часть заявок будет потеряна по причине ухода «нетерпеливых» клиентов из очереди.
В ходе численного эксперимента для этой модели было установлено, что если среднее время ожидания подключения к Интернету составляет приблизительно от 2 мин до 10 мин, то при увеличении λ процент потерянных заявок будет расти при условии постоянной интенсивности обслуживания. Следовательно, администратор системы может вмешаться в работу, если решит уменьшить процент потерянных заявок путем установки ограничений в пребывании пользователей в системе.
4. Администратор устанавливает конкретное время пребывания при достижении которого заявка удаляется из системы. При этой модели входной поток случайно, а внутри системы он становится детерминированным
В этой модели представляет интерес оценка вероятности подключения клиента к сети Интернет непосредственно в момент обращения. Ниже приведено расчетное соотношение для вычисления этой величины.
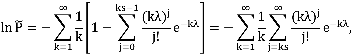
где s – допустимое число одновременных подключений к сети Интернет, т.е. число каналов.
Посредством численного эксперимента, установлено, что при увеличении интенсивности входного потока λ заявок/час при конкретных заданных параметрах, (лимитированное время подключения пользователя к сети Интернет и допустимое количество одновременных подключений
и допустимое количество одновременных подключений 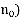 администратор системы может повлиять на работоспособность системы путем увеличения технических ресурсов системы, а в случае невозможности, указать меньшее значение времени подключения к сети Интернет
администратор системы может повлиять на работоспособность системы путем увеличения технических ресурсов системы, а в случае невозможности, указать меньшее значение времени подключения к сети Интернет .
.
В результате проделанной работы и составления критических показателей во время численного эксперимента, были выявлены варианты эффективного управления, т.е. режима администрирования системы для каждого конкретного случая. Основываясь на полученных результатах, программисту можно реализовать прикладной программный продукт, который в зависимости от ситуации и поведения пользователей системы сможет решить проблему «поглощающего состояния» беспроводного доступа в сеть Интернет путем «решающих правил».
Литература:
Ахметшин Д.А., Курмангалиев, Д.Р. Концепция использования промежуточных сетей передачи данных при организации публичного доступа в сеть Интернет // Вестник КГТУ. – 2011. №24. – С. 56-59.
Ахметшин Д.А., Печеный Е.А., Нуриев Н.К. Математическое моделирование системы аппаратно-программного комплекса промежуточной сети передачи данных // Вестник КГТУ. – 2014. №4. – С. 283-285.
Ахметшин Д.А., Печеный Е.А., Нуриев Н.К. Математическое и имитационное моделирование работы системы беспроводной передачи данных с вырожденным потоком обслуживания // Вестник КГТУ. – 2014. №10. – C. 216-221.
Ахметшин Д.А. Использование промежуточных беспроводных сетей передачи данных с учетом географического положения пользователя // Фундаментальные исследования. – 2014. – № 6 (часть 5) . – С. 1163-1166.