Математическое и имитационное моделирование работы системы беспроводной передачи данных с вырожденным потоком обслуживания
Выходные данные:
Ахметшин, Д.А. Математическое и имитационное моделирование работы системы беспроводной передачи данных с вырожденным потоком обслуживания / Д.А. Ахметшин, Е.А. Печеный, Н.К. Нуриев // Вестник Казанского технологического университета. – 2014. №10 – С. 216-221.
УДК 004.4
Д.А. Ахметшин, Е. А. Печеный, Н.К. Нуриев
МАТЕМАТИЧЕСКОЕ И ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ РАБОТЫ СИСТЕМЫ БЕСПРОВОДНОЙ ПЕРЕДАЧИ ДАННЫХ С ВЫРОЖДЕННЫМ ПОТОКОМ ОБСЛУЖИВАНИЯ
Ключевые слова: беспроводные сети, Интернет, информация, бизнес, образование, компьютеры, передача данных, общество, теория массового обслуживание, численный эксперимент
Рассматриваются существующие тенденции передачи данных в глобальных сетях и беспроводных сетях, предлагается способ организации информационного пространства через систему аппаратно-программного комплекса промежуточной сети передачи данных при организации публичного доступа в сеть Интернет по технологии Wi-Fi, целью которого является предоставление доступа к сети Интернет. Характерной особенностью систем подобного типа является ограничение времени пребывания пользователей в сети, вследствие чего обслуживание Интернет – пользователей напрямую зависит от количества клиентов, подключенных к промежуточной сети. Посредством натурного эксперимента на действующей системе было установлено предельное число подключений к Интернет, при котором всем пользователям может быть назначено конкретное время пребывания в сети.
Keywords: wireless networks, Internet, information, business, education, computers, data, community, queuing theory, numerical experiment
Discusses current trends in the global data networks and wireless networks , a method for organizing information space through the hardware-software complex intermediate data network in the organization of public Internet access technology Wi-Fi, which aims to provide access to the Internet. A characteristic feature of this type of systems is to limit the residence time of users on the network , so that Internet service - people are directly dependent on the number of clients connected to theintermediate network . Through a natural experiment on the current system was established limit on the number of connections to the Internet , in which all users can be assigned a specific time stay in the network .
Не будет преувеличением сказать, что начало 21 века характеризуется прежде всего бурным развитием информационных и, в частности, Интернет-технологий. Это привело к широкому распространению беспроводных промежуточных сетей передачи данных, которые позволяют обеспечить доступ в Интернет большому количеству пользователей одновременно. Подобная услуга оказывается востребованной в образовании [8] и актуальной в производственных помещениях и офисах крупных компаний, ресторанах и кафе, транспортных пассажирских терминалах и других местах, где наблюдается большое скопление людей.
Базовым инструментом количественного анализа таких сетей является теория массового обслуживания с ее весьма совершенным и глубоко проработанным аппаратом. Отличительной особенностью беспроводных сетей передачи данных, как систем массового обслуживания, служит, то обстоятельство, что они не имеют канал обслуживания в их традиционном понимании, т.е. специалистов или технических устройств, существующих вне зависимости от наличия или отсутствия требований. Формирование каналов происходит по мере поступления требований и каждый новый клиент, подключенный к Интернет посредством сети, фактически создает новый канал, отбирая часть возможностей сети под обеспечения своего трафика [1,3].
Естественно, что интенсивность обслуживания (скорость передачи информации пользователям) будет непосредственно зависеть от числа сформированных каналов, иначе говоря, от числа клиентов, одновременно воспользовавшихся услугами данной сети для выхода в Интернет. Поэтому для обеспечения приемлемых условий абонентам сети, администратор должен принимать необходимые меры по ограничению числа одновременных подключений к Интернет, сообразуясь с техническими характеристиками сети и объемом трафика [4-6,8].
Если вмешательство администратора ограничивается только наблюдением за тем, чтобы число одновременных подключений к Интернет не превышало заранее установленного порогового значения, то справедливой можно считать гипотезу о том, что и входной поток клиентов и поток обслуживания являются пуассоновскими. В этом случае все параметры, характеризующие функциональные возможности беспроводной сети, как системы массового обслуживания, можно найти с помощью известных расчетных соотношений, что и было сделано в работе [2]. Однако, если администратор коммерческой сети ставит цель расширения клиентской базы и сокращение времени ожидания в очереди, а администратор сети, задействованной в производственной сфере, хочет ограничить использование Интернет сотрудниками, может быть установлено фиксированное время  , по истечению которого пользователь отключается от сети.
, по истечению которого пользователь отключается от сети.
Это переводит систему в качественно новое состояние, поскольку поток обслуживания перестает быть случайным, а его интенсивность для всех клиентов оценивается постоянной величиной 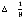 . Подобные потоки носят название вырожденных.
. Подобные потоки носят название вырожденных.
По классификации Кендалла системы массового обслуживания такого типа относятся к классу M/D/s, где M означает, что входной поток требований является пуассоновским; D – что поток обслуживания вырожден; s – число, соответствующее количеству каналов обслуживания (в нашем случае максимальное допустимое числу одновременных подключений). Дадим математическое описание процесса функционирования такой системы.
Рассмотрим пуассоновский поток клиентов с интенсивностью  , поступающий на вход беспроводной сети, в которой может быть обеспечена комфортная работа не более s пользователей одновременно. Если положить
, поступающий на вход беспроводной сети, в которой может быть обеспечена комфортная работа не более s пользователей одновременно. Если положить 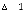 , то обязательным условием нормальной работы сети, исключающим возможность неограниченного накопления требований в очереди, будет
, то обязательным условием нормальной работы сети, исключающим возможность неограниченного накопления требований в очереди, будет 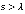 . Обозначим
. Обозначим 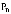 - вероятность того, что в некоторый момент времени в системе (подключены к Интернет и ожидают в очереди) находятся n клиентов, а
- вероятность того, что в некоторый момент времени в системе (подключены к Интернет и ожидают в очереди) находятся n клиентов, а 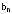 - вероятность того, что в системе находится не более n клиентов. Иначе говоря
- вероятность того, что в системе находится не более n клиентов. Иначе говоря
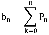
Вследствие постоянства времени обслуживания, вероятность того, что к окончанию единичного временного интервала в системе будет некоторое определенное число клиентов можно выразить через вероятности числа клиентов в системе на начало единичного интервала, умноженные на вероятности поступления в течении этого интервала того или иного числа новых клиентов. Очевидно, что все клиенты, которые были подключены к Интернет на момент начало данного интервала покинут систему к его окончанию.
Замечания, сделанные о характере входного потока заявок и потока обслуживания приводят к системе уравнений
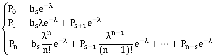
Первое уравнение соответствует ситуации когда очереди нет, т.е. в начале единичного временного интервала в сети находилось не более s клиентов, каждый из которых был подключен к Интернет, а в течение интервала появления новых клиентов отмечено не было. Второе уравнение соответствует случаю, когда на начало интервала в сети находилось не более s клиентов, а в его течение было зарегистрирован еще один клиент, помещенный в очередь; если в начале интервала были задействованы все s допустимых подключений, один клиент находился в очереди, а в ходе интервала новые клиенты не появлялись. Множитель 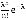 имеет смысл пуассоновской вероятности регистрации n новых клиентов в течение единичного интервала.
имеет смысл пуассоновской вероятности регистрации n новых клиентов в течение единичного интервала.
Введем в рассмотрение функцию 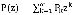 , где z в общем случае является комплексным переменным. Функции такого типа традиционно используются для анализа и решения систем уравнений подобного вида и носят название производящих функций. Совершенно очевидно, что P(1)=1.
, где z в общем случае является комплексным переменным. Функции такого типа традиционно используются для анализа и решения систем уравнений подобного вида и носят название производящих функций. Совершенно очевидно, что P(1)=1.
Обозначим 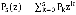 . Тогда, умножив каждое из уравнений системы на z в соответствующей степени и просуммировав, получим
. Тогда, умножив каждое из уравнений системы на z в соответствующей степени и просуммировав, получим
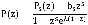
Поскольку 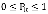 , внутри единичного круга |z|<1 функция P(z) будет регулярной и ограниченной. Следовательно внутри единичного круга и на его окружности числитель имеет нули, в число которых входят все нули знаменателя в этой области. Из теории функций комплексного переменного известно (Теорема Руше), что число таких нулей равно s. Обозначим их как
, внутри единичного круга |z|<1 функция P(z) будет регулярной и ограниченной. Следовательно внутри единичного круга и на его окружности числитель имеет нули, в число которых входят все нули знаменателя в этой области. Из теории функций комплексного переменного известно (Теорема Руше), что число таких нулей равно s. Обозначим их как 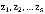 . Нетрудно заметить, что одним из нулей является число 1. Так как числитель есть многочлен степени s, он может быть представлен как
. Нетрудно заметить, что одним из нулей является число 1. Так как числитель есть многочлен степени s, он может быть представлен как 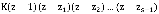 . Константа К находится из условий
. Константа К находится из условий
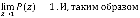
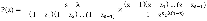
В силу структуры производящей функции P(z), вероятности состояний сети 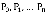 определяется как коэффициенты разложений функции P(z) в степенной ряд при соответствующих степенях z.
определяется как коэффициенты разложений функции P(z) в степенной ряд при соответствующих степенях z.
Выясним некоторые важные характеристики беспроводной сети, относящихся к типу M/D/s. В вероятности того, что клиент, обратившийся к услугам системы в случайным момент времени t, будет сразу же подключен к Интернет. Фактически это означает, что к этому моменту времени число клиентов, находящихся в системе меньше числа допустимых подключений s и прибытие нового клиента не инициирует формирование очереди. Обозначим эту вероятность  . Она равна сумме вероятностей того, что число задействованных подключений меньше s. Таким образом
. Она равна сумме вероятностей того, что число задействованных подключений меньше s. Таким образом
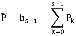
Введем в рассмотрение еще одну производящую функцию 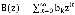 . В соответствии с принятыми обозначениями
. В соответствии с принятыми обозначениями 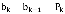 . Отсюда очевидно
. Отсюда очевидно 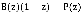 , или
, или 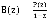 . Поскольку выражение для функции P(z) получено,
. Поскольку выражение для функции P(z) получено, 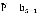 вычисляется как коэффициент при
вычисляется как коэффициент при 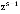 в разложении функции B(z), который равен K. Следовательно
в разложении функции B(z), который равен K. Следовательно
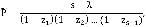
или после логарифмирования
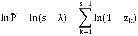
Саати [9] указывает, ссылаясь в свою очередь на результаты, полученные Кроммелином [11] и Поллачеком [12], что решение этого уравнения сводится к вычислению интеграла
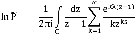
где C – замкнутый единичный контур, охватывающий точку z=1, а 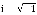 . Ряд, входящий в состав подынтегрального выражения, сходится, так как на контуре C
. Ряд, входящий в состав подынтегрального выражения, сходится, так как на контуре C
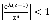 ,
,
поэтому
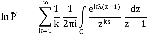
Подынтегральная функция имеет полюс порядка ks в точке z=0 и полюс первого порядка в точке z=1. Обратимся к теории вычетов, которая утверждает, что если точка  является полюсом функции g(z) порядка n, то вычет равен произведению
является полюсом функции g(z) порядка n, то вычет равен произведению 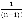 на (m-1) – ую производную функции
на (m-1) – ую производную функции 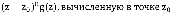 . Просуммировав все вычеты найдем окончательный результат. Учитывая, что
. Просуммировав все вычеты найдем окончательный результат. Учитывая, что
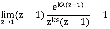
Получим
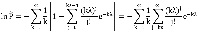
Финальная вероятность 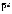 , характеризующая стационарное состояние, которое достигается при
, характеризующая стационарное состояние, которое достигается при 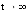 , имеет смысл доли клиентов, получивших подключение к Интернет сразу же после прохождения процедуры регистрации. Величина
, имеет смысл доли клиентов, получивших подключение к Интернет сразу же после прохождения процедуры регистрации. Величина  имеет смысл доли клиентов вынужденных до получения доступа к Интернет провести какое то время в очереди.
имеет смысл доли клиентов вынужденных до получения доступа к Интернет провести какое то время в очереди.
Использование полученного результата в практике инженерных расчетов затруднительно, так как для этого требуется нахождение суммы двойного бесконечного ряда. Это обуславливает необходимость поиска иных инструментов исследования подобных систем, наиболее перспективным из которых представляется аппарат имитационного моделирования и статистического анализа [10].
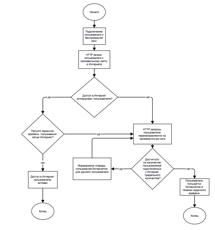
Рис. 1. Схема работы системы
В расчете будем случайный образом менять значения лимитированного времени подключения пользователя к сети Интернет  , интенсивность входного потока λ - количество заявок в час и количество одновременных пользователей системы k. Для расчета подобной модели проведем численный эксперимент, а именно оценим вероятность того, что за время t в систему обратится k клиентов. Поскольку входной поток заявок предполагается пуассоновским, вероятность может быть вычислена по известной формуле
, интенсивность входного потока λ - количество заявок в час и количество одновременных пользователей системы k. Для расчета подобной модели проведем численный эксперимент, а именно оценим вероятность того, что за время t в систему обратится k клиентов. Поскольку входной поток заявок предполагается пуассоновским, вероятность может быть вычислена по известной формуле
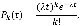
Для расчета были использованы следующие данные:
Лимитированное время подключения пользователя к сети Интернет для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин.
для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин.
Интенсивность входного потока λ - количество заявок в час, зависит от времени суток, среднее наблюдаемое значение λ в течении рабочего времени, для экспериментального подсчета значение λ=40.
Предельное количество одновременных подключений к сети Интернет  .
.
Результаты расчета приведены в таблице: Таблица 1. Экспериментального подсчет при λ=40.
|
|
λ (интенсивность заявок в час) |
%, что каждая случайная заявка попадет в очередь |
|
5 |
40 |
- |
|
10 |
40 |
- |
|
15 |
40 |
0,05 |
|
20 |
40 |
3,01 |
|
25 |
40 |
17,01 |
|
30 |
40 |
43,97 |
|
35 |
40 |
71,28 |
|
40 |
40 |
88,68 |
Во второй таблице приведены результаты расчета с другим значением интенсивности входного потока клиентов λ=45.
Лимитированное время подключения пользователя к сети Интернет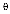 для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет
для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет  .
.
Таблица 2. Экспериментального подсчет при λ=45.
|
|
λ (интенсивность заявок в час) |
%, что каждая случайная заявка попадет в очередь |
|
5 |
45 |
- |
|
10 |
45 |
- |
|
15 |
45 |
0,48 |
|
20 |
45 |
8,15 |
|
25 |
45 |
33 |
|
30 |
45 |
65,17 |
|
35 |
45 |
87,11 |
|
40 |
45 |
96,46 |
В третей таблице приведены результаты расчета с другим значением интенсивности входного потока клиентов λ=50.
Лимитированное время подключения пользователя к сети Интернет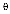 для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин.
для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин.
Предельное количество одновременных подключений к сети Интернет  .
.
Таблица 3. Экспериментального подсчет при λ=50.
|
|
λ (интенсивность заявок в час) |
%, что каждая случайная заявка попадет в очередь |
|
5 |
50 |
- |
|
10 |
50 |
- |
|
15 |
50 |
1,6 |
|
20 |
50 |
17,07 |
|
25 |
50 |
51,34 |
|
30 |
50 |
81,4 |
|
35 |
50 |
95,17 |
|
40 |
50 |
99,09 |
В четвертой таблице приведены результаты расчета с другим значением интенсивности входного потока клиентов λ=55.
Лимитированное время подключения пользователя к сети Интернет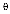 для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет
для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет  .
.
Таблица 4. Экспериментального подсчет при λ=55.
|
|
λ (интенсивность заявок в час) |
%, что каждая случайная заявка попадет в очередь |
|
5 |
55 |
- |
|
10 |
55 |
- |
|
15 |
55 |
3,97 |
|
20 |
55 |
29,5 |
|
25 |
55 |
68,3 |
|
30 |
55 |
91,36 |
|
35 |
55 |
98,45 |
|
40 |
55 |
99,8 |
В пятой таблице приведены результаты расчета с другим значением интенсивности входного потока клиентов λ=60.
Лимитированное время подключения пользователя к сети Интернет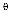 для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет
для экспериментального подсчета будем менять в интервале 5-40 мин. с шагом 5 мин. Предельное количество одновременных подключений к сети Интернет  .
.
Таблица 5. Экспериментального подсчет при λ=60.
|
|
λ (интенсивность заявок в час) |
%, что каждая случайная заявка попадет в очередь |
|
5 |
60 |
- |
|
10 |
60 |
0,05 |
|
15 |
60 |
8,15 |
|
20 |
60 |
43,97 |
|
25 |
60 |
81,4 |
|
30 |
60 |
96,46 |
|
35 |
60 |
99,56 |
|
40 |
60 |
99,96 |
На основе выше полученных результатов построены следующие графики
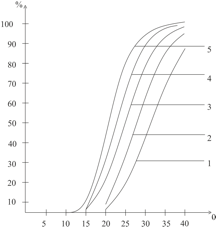
Рис.2. Граф работы системы при различных λ
По результатам численного эксперимента, как показано на Рис.1. наблюдается, что для кривой 1 при 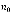 = 20, интенсивность входного потока λ = 40 заявок/час и заданным временем пребывания в системе
= 20, интенсивность входного потока λ = 40 заявок/час и заданным временем пребывания в системе 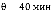 вероятность того, что очередная заявка попадет в очередь составит 88,68%. Для кривой 2, при
вероятность того, что очередная заявка попадет в очередь составит 88,68%. Для кривой 2, при 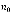 = 20, интенсивность входного потока λ = 45 заявок/час и заданным временем пребывания в системе
= 20, интенсивность входного потока λ = 45 заявок/час и заданным временем пребывания в системе 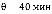 вероятность того, что очередная заявка попадет в очередь составит 96,46%. Для кривой 3, при
вероятность того, что очередная заявка попадет в очередь составит 96,46%. Для кривой 3, при 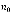 = 20, интенсивность входного потока λ = 50 заявок/час и заданным временем пребывания в системе
= 20, интенсивность входного потока λ = 50 заявок/час и заданным временем пребывания в системе 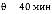 вероятность того, что очередная заявка попадет в очередь составит 99,09%.
вероятность того, что очередная заявка попадет в очередь составит 99,09%.
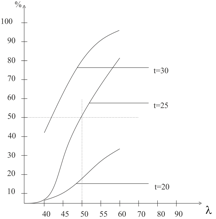
Рис.3. Графики работы системы при различных времени пребывания t
В зависимости от ситуации, допустимый предел попадания заявки в очередь может быть различным. Например, установим допустимый предел попадания заявки в очередь в 50 %. На Рис. 3. можно увидеть, при указанным времени пребывания t=25 и интенсивности входного потока λ >50 заявок в час, в системе достигнут допустимый предел попадания очередной заявки в очередь. Таким образом администратор системы, использовав результаты имитационного моделирования, самостоятельно может для работы системы задать критичный процент заявок, попавших в очередь, и при увеличении интенсивности входного потока λ заявок/час, администратор системы может принять срочные меры, а именно уменьшить лимитированное время подключения пользователя к сети Интернет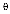 .
.
Следовательно, в результате численного эксперимента, реализованного с помощью имитационной модели, установлено, что при увеличении интенсивности входного потока λ заявок/час при конкретных заданных параметрах, лимитированное время подключения пользователя к сети Интернет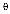 и допустимое количество одновременных подключений
и допустимое количество одновременных подключений 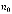 , администратор системы может повлиять на работоспособность системы путем увеличения технических ресурсов системы, а в случае невозможности, указать меньшее значение времени подключения к сети Интернет
, администратор системы может повлиять на работоспособность системы путем увеличения технических ресурсов системы, а в случае невозможности, указать меньшее значение времени подключения к сети Интернет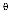 .
.
Список используемой литературы:
1. Ахметшин Д.А., Курмангалиев Д.Р. Концепция использования промежуточных сетей передачи данных при организации публичного доступа в сеть Интернет // Вестник КГТУ. – 2011. №24. – С. 56-59
2. Ахметшин Д.А., Печеный Е.А., Нуриев Н.К. Математическое моделирование системы аппаратно-программного комплекса промежуточной сети передачи данных // Вестник КГТУ. – 2014. №4. – С. 283-285
3. Ахметшин Д.А. ЭСКИЗНЫЙ ПРОЕКТ АППАРАТНО-ПРОГРАММНОГО КОМПЛЕКСА ПРОМЕЖУТОЧНОЙ СЕТИ ПЕРЕДАЧИ ДАННЫХ // Современные проблемы науки и образования. – 2014. – № 2;
4. Ахметшин Д.А. ИСПОЛЬЗОВАНИЕ ПРОМЕЖУТОЧНЫХ БЕСПРОВОДНЫХ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ С УЧЕТОМ ГЕОГРАФИЧЕСКОГО ПОЛОЖЕНИЯ ПОЛЬЗОВАТЕЛЯ // Фундаментальные исследования. – 2014. – № 6 (часть 6).
5. Ахметшин, Д.А. Программно-аппаратная система для беспроводного доступа в Интернет по технологии Wi-Fi с функцией принудительной демонстрации рекламных материалов для получении прибыли: монография / Д.А. Ахметшин, Д.Р. Курмангалиев – Казань: Изд-во Центр инновационных технологий, 2009. – 87 с.
6. Курмангалиев Д.Р., Ахметшин Д.А. Применение терминальных устройств с сенсорным дисплеем в образовательном процессе // Вестник Казанского государственного технологического университета - № 24. – 2011 – С. 59 – 63.
7. Курмангалиев Д.Р., Ахметшин Д.А. Применение Беспроводных технологий для увеличения прибыли коммерческих организаций В Сфере обслуживания // X Всероссийская научно-практическая конференция студентов, аспирантов и молодых ученых с международным участием Молодежь и современные информационные технологии Россия, г. Тула 2011.
8. Нуриев Н.К., Старыгина С.Д., Ильмушкин Г.М., Шайдуллина Н.К. Проектирование дидактических систем нового поколения с использованием облачных технологий // Educational Technology & Society – 2013 (http://ifets.ieee.org/russian/periodical/journal.html) - V.16. - N 4. – С. 412-429 c. – ISSN 1436-4522.
9. Саати, T.JI. Элементы теории массового обслуживания и ее применение / T.J1. Саати. М.: Советское радио, 1971. - 520 с.
10. Титов А.Н., Нуриев Н.К., Тазиева Р.Ф. Оценка параметров вероятностной модели по экспериментальным данным // Вестник Казанского технологического университета. – Казань, 2013. – Т.16. – №19. – С. 324-330.
11. Crommelin C. D. Delay probability formulae when the holding times are constant. Post Office Electrical Engineer's Journal. 1932. V.25. P. 41-50.
12. Palm C. Palm C., Intensitatsschwankungen im Fernsprechverkehr. Ericsson Technics. 1943. № 44. P. 1-189.
Сведения об авторах:
Ахметшин Д.А. Ассистент, кафедра информатики прикладной математики ФГБОУ ВПО «КНИТУ», dinar@ahmetshin.com
Нуриев Н.К. д.п.н, профессор, кафедра информатики прикладной математики ФГБОУ ВПО «КНИТУ» nurievnk@mail.ru
Печеный Е. А. к.т.н., доцент, кафедра информатики прикладной математики ФГБОУ ВПО «КНИТУ»
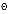 , мин
, мин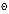 , мин
, мин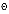 , мин
, мин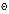 , мин
, мин , мин
, мин